Exercise 1

For the correct plot of the true/approximated derivatives...

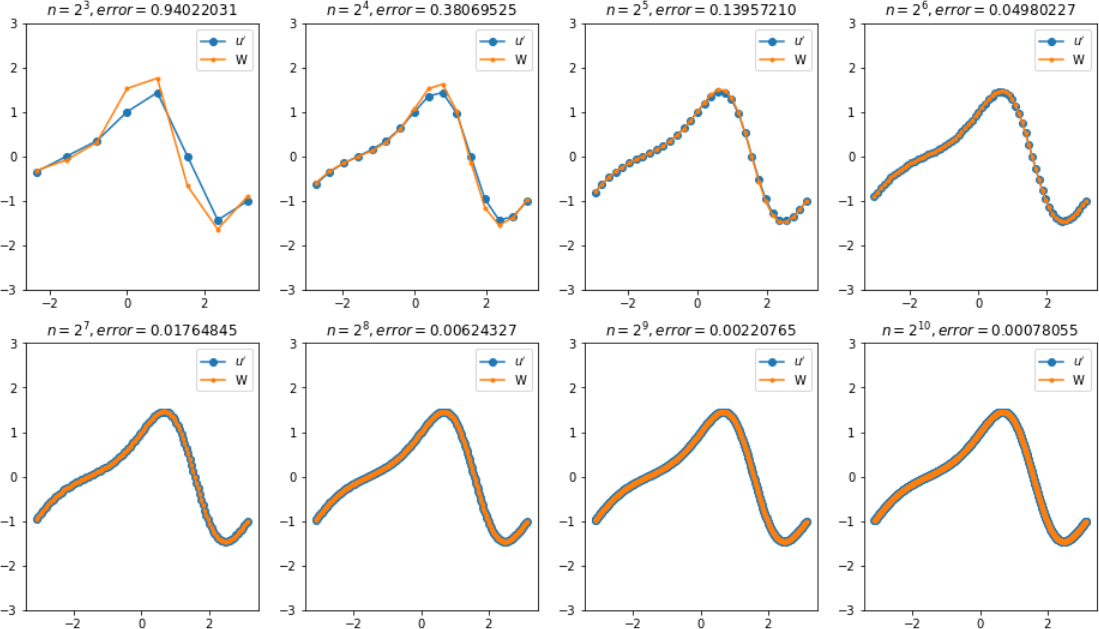
If there is some peak occurs at the boundary, then it may be caused by the wrong boundary processing.

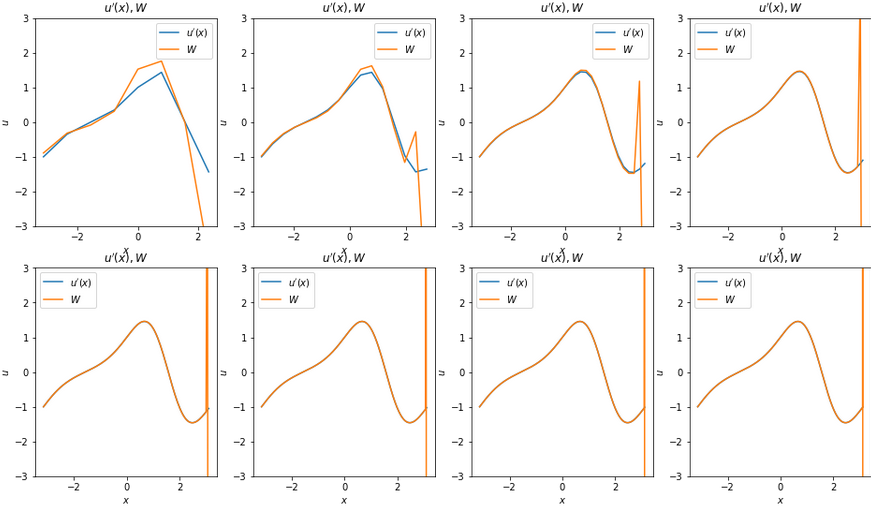
Peroidic Boundary Condition

Check your differentiation matrix!

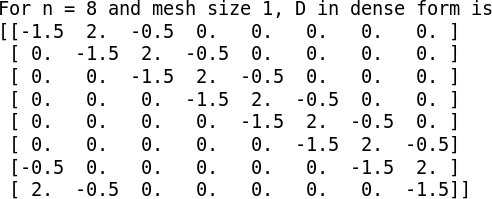
Note the bottom left part!

Peroidic Boundary Condition

Also check your mesh don't cover both end points!
You can choose one of the ways below.

And for the correct plot to observe
the rate of convergence...

You can choose 2-norm/mean squared error/etc. as the metric.
For example, if using 2-norm, you can find the below behavior.

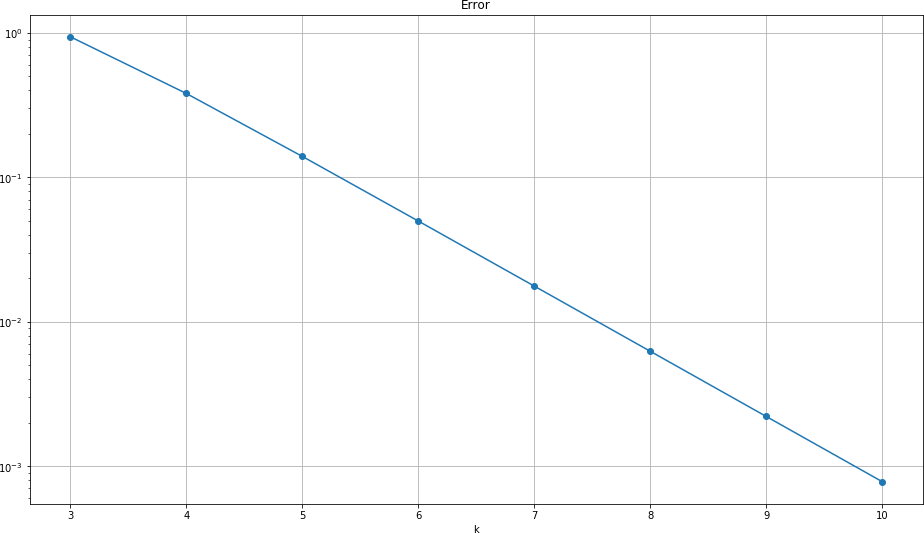
So it looks like it converges linearly,
but how do we ensure it?

Let's clarify the rate of convergence first.

Given a sequence $x_k$ which converges to $L$ and denote the error $(L - x_k)$ by $e_k$.
Then the rate of convergence is defined by

$$\lim_{k\to\infty}\frac{|e_{k+1}|}{|e_k|}=c.$$

And can be categorized into 3 cases

Order of Convergence

$$\lim_{k\to\infty}\frac{|e_{k+1}|}{|e_k|^n} < M \in (0, \infty)$$

• n=1 is called linear convergence
  (but note that $\frac{|e_{k+1}|}{|e_k|}\equiv c \in (0, 1)$ is called geometric convergence)
• n>1 is called superlinear, e.g. the order of tangent method is golden ratio.
• n=2 is called quadratic convergence, e.g. Newton method
• n=3 is called cubic convergence
• etc.

And a sequence is called Converge Logarithmically if

Also you can distinguish them roughly by the plot

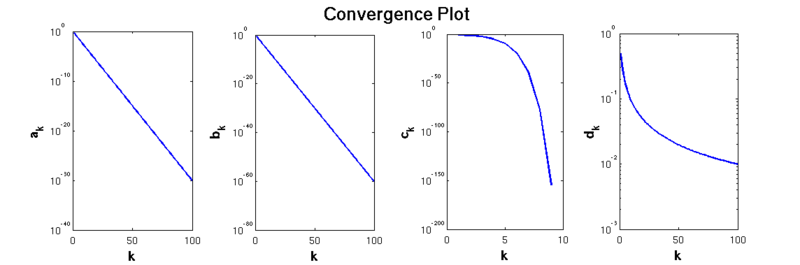
From left to right: linearly, linearly, superlinearly, sublinearly (Ref. Wikipedia)

Now let's go back to the exercise.

You can evaluate the rate of convergence by the following sample code.

(Here we use 2-norm as example)

So the rate of convergence is about 0.35356615, which is about $2^{-3/2}$

So... the right answer is "it converges linearly."
(NOT superlinearly, sublinearly, logarithmically...)

But can we derive this constant by hand?

We know for the one-sided 3-point differentiation approximation

$$f'(x) \approx g(x) \triangleq \alpha_1 f(x) + \alpha_2 f(x+h) + \alpha_3 f(x+2h)$$

can be derived by using the Taylor expansion and then solving the linear system $$\begin{aligned} f(x) &= f(x)\\ f(x+h) &= f(x) + hf'(x) + \frac{h^2}{2}f''(x) + O(h^3)\\ f(x+2h) &= f(x) + 2hf'(x) + \frac{4h^2}{2}f''(x) + O(h^3) \end{aligned}$$

After you find the solution $$\alpha_1 = -\frac{3}{2h}, \alpha_2 = \frac{2}{h}, \alpha_3=-\frac{1}{2h}$$

If we choose 2-norm as the error metric, then the error is $$e_k = \left(\sum_{j=1}^n (f'(x_j)-g(x_j))^2\right)^{\frac{1}{2}} = \sqrt{n (O(h^2)^2)} = 2^{\frac{k}{2}}O((2\pi)^2 2^{-2k}),$$ where $n=2^k, k=3 \dots 10$ is the number of mesh points and $h$ is the mesh size $h=\frac{2\pi}{n}$

Then the rate of convergence in the 2-norm case is $$\lim_{k\to\infty}\frac{|e_{k+1}|}{|e_k|} = 2^{-\frac{3}{2}},$$ which coincides with the numerical result.

In addition, you can check the case of using mean squared error as the error metric, $$e_k = \frac{1}{n}\left(\sum_{j=1}^n (f'(x_j)-g(x_j))^2\right) = O(h^2)^2 = O((2\pi)^4 2^{-4k}),$$ where $n=2^k, k=3 \dots 10$ is the number of mesh points and $h$ is the mesh size $h=\frac{2\pi}{n}$

Then the rate of convergence in mean squared error is $$\lim_{k\to\infty}\frac{|e_{k+1}|}{|e_k|} = 2^{-4}$$

And the numerical result also supports the theoretical analysis.

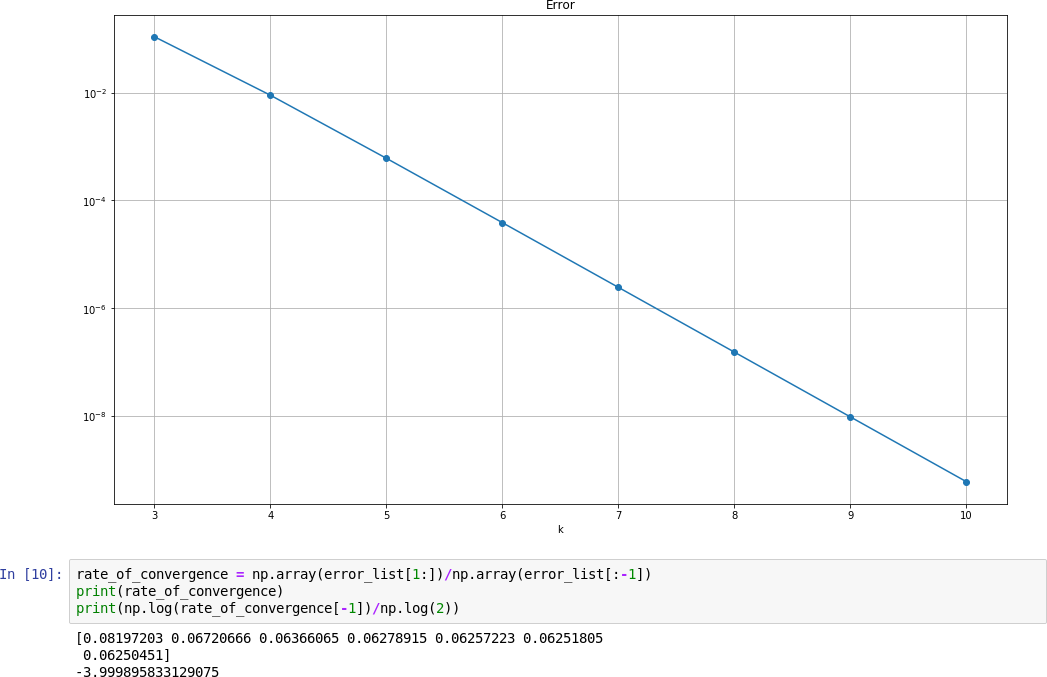
(Use MSE as the error metric)

Exercise 2

For comparison of which one is the best method,
you may need use the exact value of the integral.

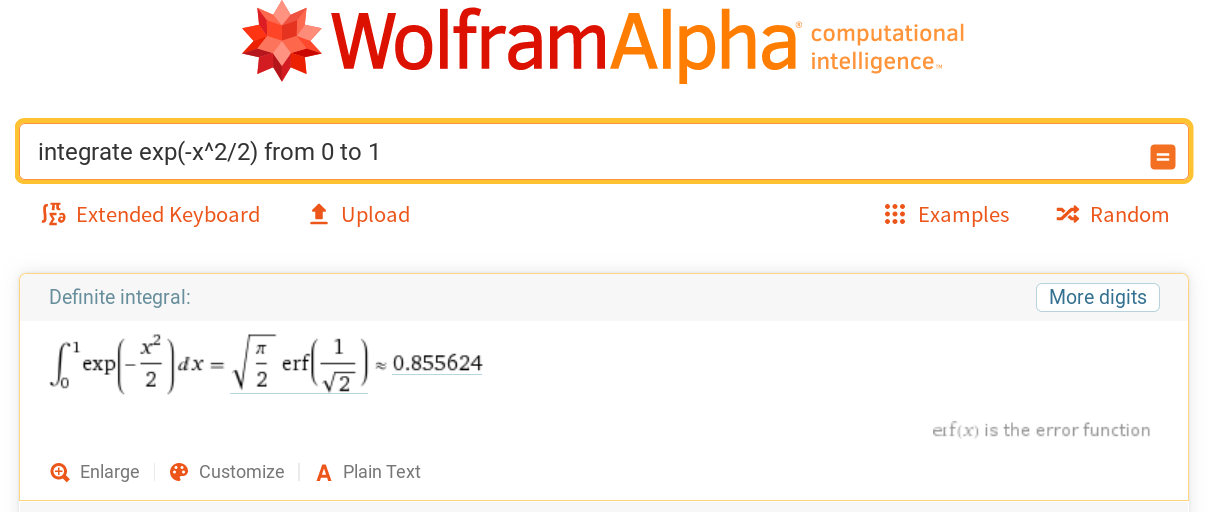
WolframAlpha is a good tool to calcualte integral like this.

So you can find the most accurate method is the Simpson's method.

Note that the implementation of Gauss-Legendre requires the parameter $n$ as the number of points (and this $n$ also means the order of used Legendre polynomials).

So it should be "p_roots(n)" instead of "p_roots(n+1)"!

This $n$ is different from the notation in our lecutre note.
In teacher's note, $n$ means $n$ partition with $n+1$ points.

Anyway, if you use $n$ points in Gauss-Legendre method, then it have degree of exactness $2n-1$. And there are $n$ weights and $n$ nodes(points) in the quadrature formula, which can be easily obtained from the table.

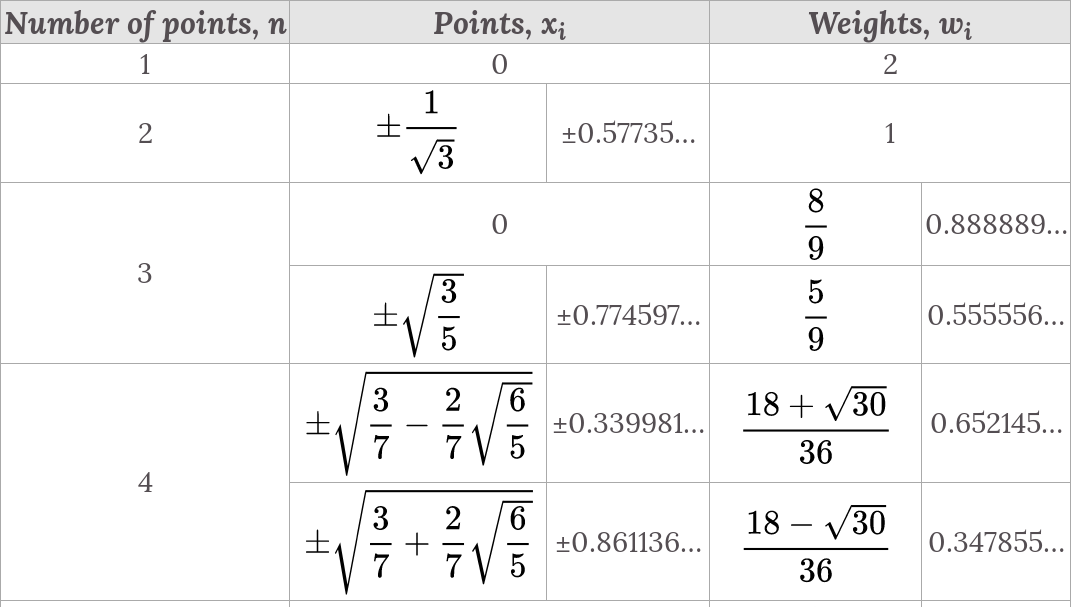
(Ref. Wikipedia)