Lab 2 Exercise Review

Exercise 1

• Since there is no root is at specific range. e.g. there is no roots for case c = 0,1. Actually, we may need to rigorously write down the proof.
• For case c=3, there are two roots to be found.
• Don't simply say "agree with the theoretical analysis", please detail it
• Please don't duplicate problem cell or answer cell. You can copy code instead.
• Please obey the rules of files format. Otherwise our judging system will fail.

Exercise 2

• Write down your proof with LaTeX properly.
• Check your loop will terminate or not.

Lab 3 Exercise Review

Exercise 1

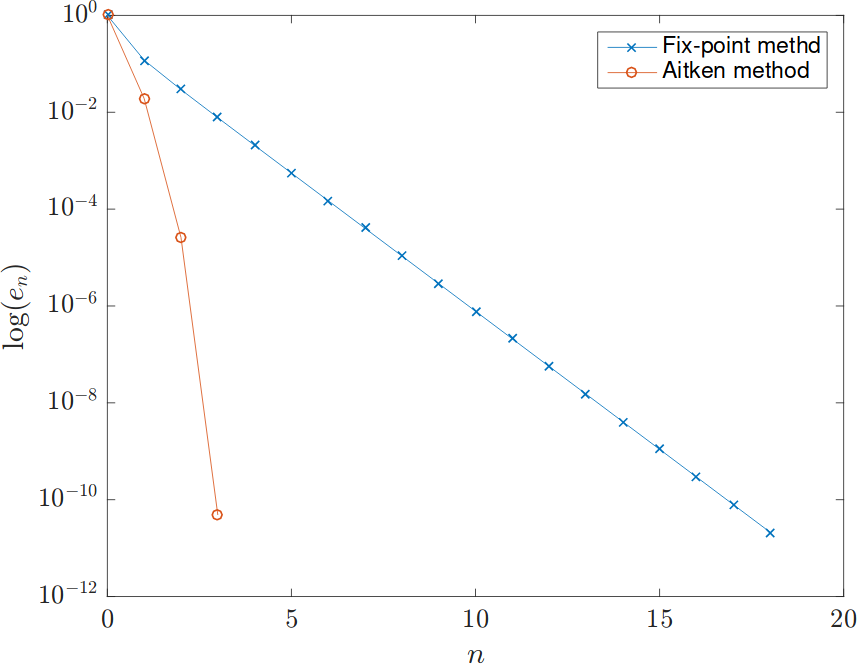
Exercise 2

Doesn't the $\omega_m$ with higher order have larger oscillation?

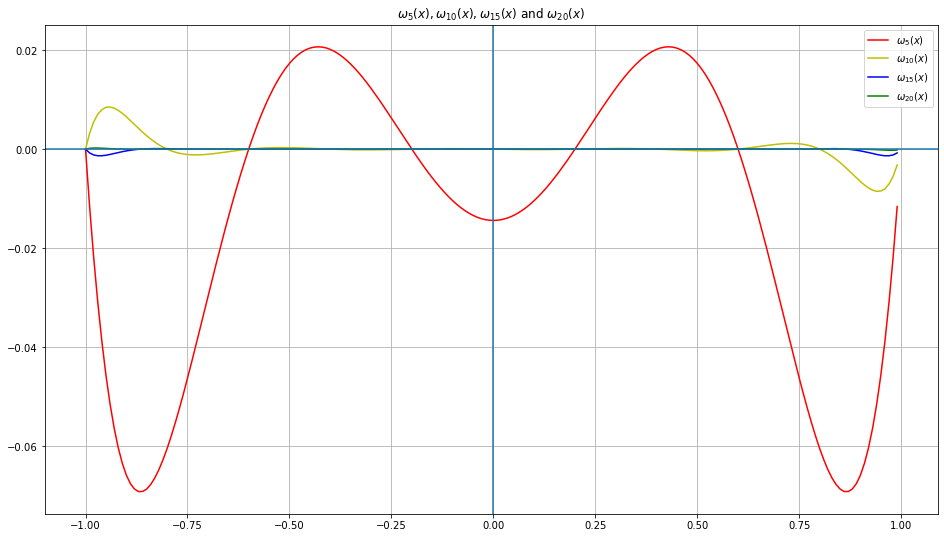
No! Runge Phenomenon means the behavior while
interpolating a function with equispaced points.

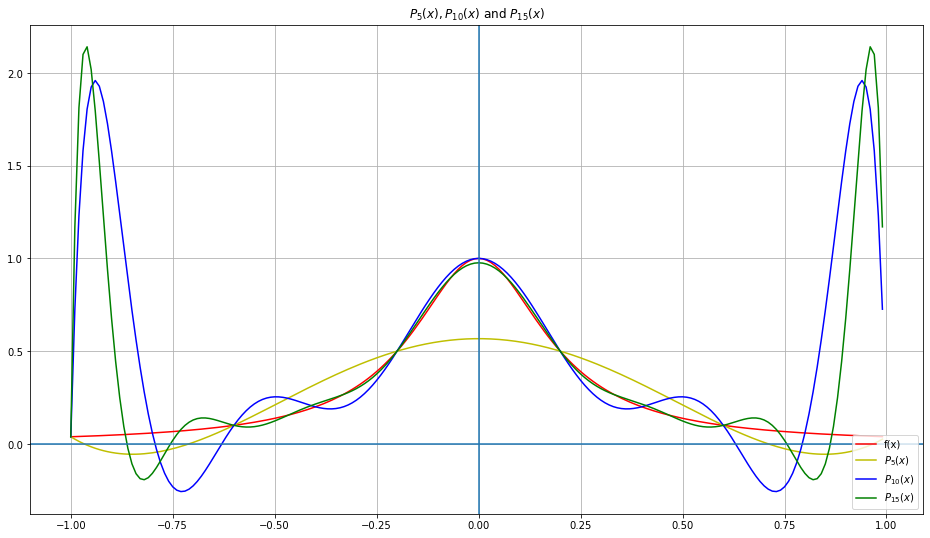
Runge function $f(x)=\frac{1}{1+25x^2}$

How to show the $\omega_m$ with higher order
has smaller oscillation?

Suppose we partition $[0,1]$ into $m$ intervals, and then compute $\omega_m(t)$
where $t$ is choosen as the point of the 2nd rightest point as below.

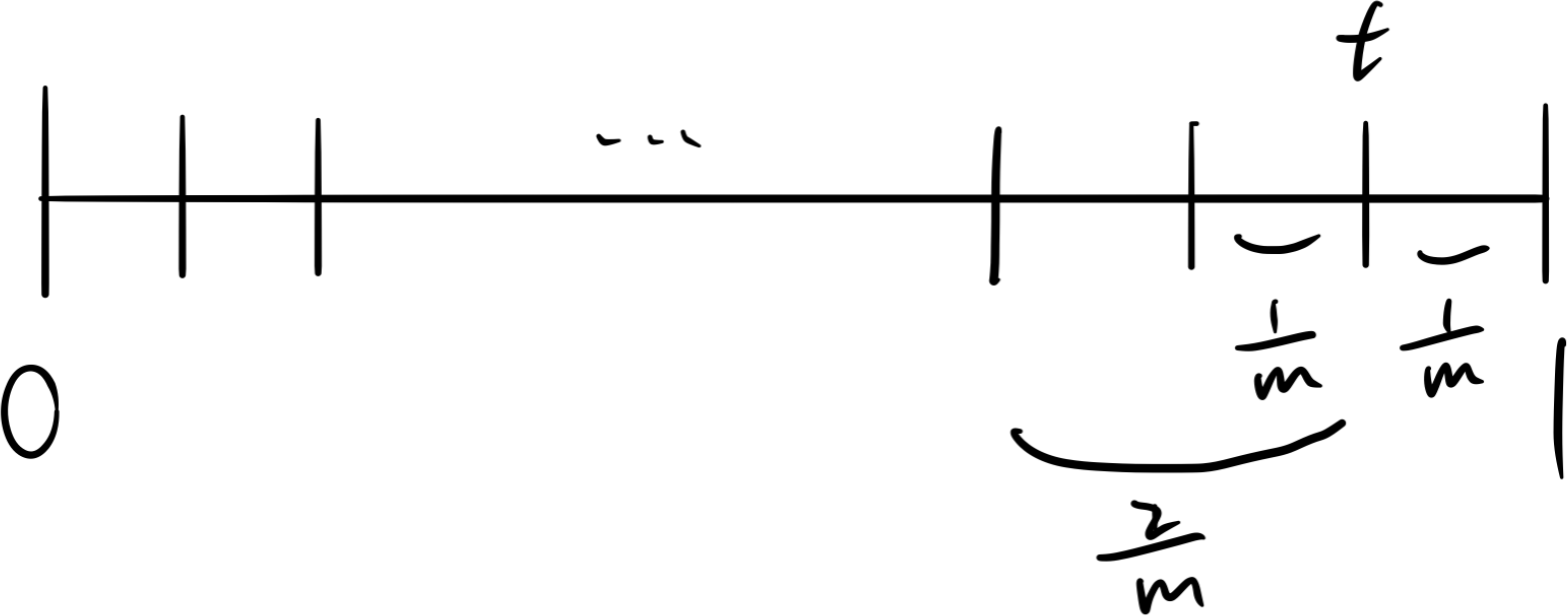
$\implies |\omega_m(t)|=\frac{1}{m}\frac{1}{m}\frac{2}{m}\dots\frac{m-2}{m}\frac{m-1}{m}$

And then we halve each $m$ intervals, and then compute $\omega_{2m}(t)$

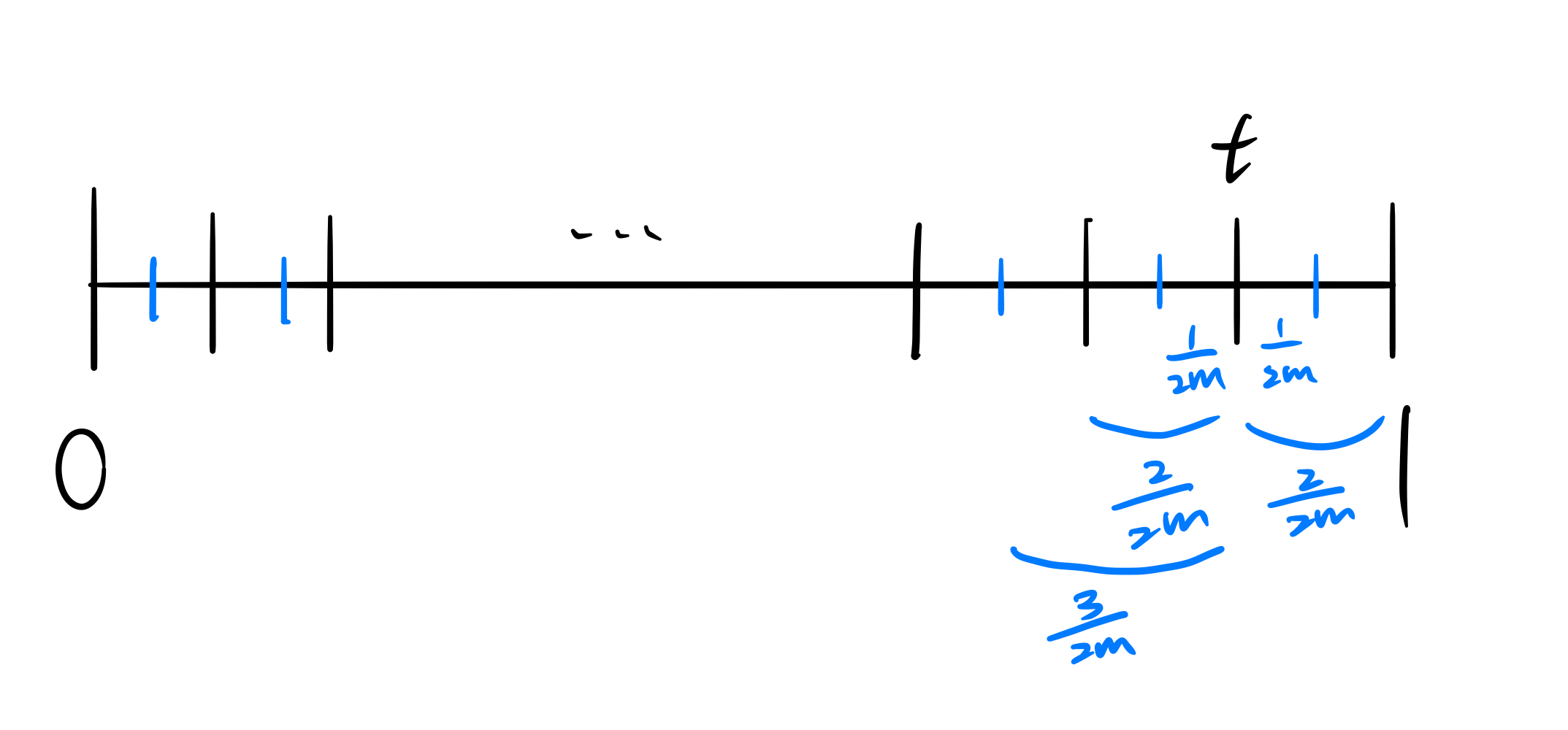
$ \implies |\omega_{2m}(t)| = (\frac{1}{2m}\frac{2}{2m}) (\frac{1}{2m}\frac{2}{2m}) (\frac{3}{2m}\frac{4}{2m}) \dots (\frac{2m-5}{2m}\frac{2m-4}{2m}) (\frac{2m-3}{2m}\frac{2m-2}{2m})\\ \leq (1\cdot\frac{2}{2m}) (1\cdot\frac{2}{2m}) (1\cdot\frac{4}{2m}) \dots (1\cdot\frac{2m-4}{2m}) (1\cdot\frac{2m-2}{2m}) = |\omega_m(t)| $

Lab 4

Numerical Differentiation

Finite Difference Approximation with 2 Points

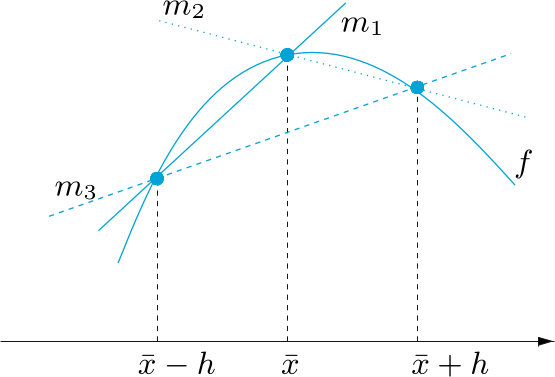
Finite Difference with 3 Points

Please open numerical-differentiation.ipynb